CONSERVATIVE AND DISSIPATIVE DISCRETISATIONS OF MULTI-CONSERVATIVE ODEs AND GENERIC SYSTEMS

Boris Andrews `|` Patrick Farrell

28.NOV.2025 (arXiv) `|` In review (CAMWA)

CHECK OUT ON ARXIV!

[…] we present two novel contributions: (i) an arbitrary-order time discretisation for general conservative ordinary differential equations that conserves all known invariants and (ii) an energy-conserving and entropy-dissipating scheme for […] differential equations written in the GENERIC format […]. We illustrate the advantages of our approximations with numerical examples of the Kepler and Kovalevskaya problems, a combustion engine model, and the Benjamin–Bona–Mahony equation.

FULL ABSTRACT

Partial differential equations (PDEs) describing thermodynamically isolated systems typically possess conserved quantities (like mass, momentum, and energy) and dissipated quantities (like entropy). Preserving these conservation and dissipation laws on discretisation in time can yield vastly better approximations for the same computational effort, compared to schemes that are not structure-preserving.

In this work we present two novel contributions: (i) an arbitrary-order time discretisation for general conservative ordinary differential equations that conserves all known invariants and (ii) an energy-conserving and entropy-dissipating scheme for both ordinary and partial differential equations written in the GENERIC format, a superset of Poisson and gradient-descent systems. In both cases the underlying strategy is the same: the systematic introduction of auxiliary variables, allowing for the replication at the discrete level of the proofs of conservation or dissipation. We illustrate the advantages of our approximations with numerical examples of the Kepler and Kovalevskaya problems, a combustion engine model, and the Benjamin-Bona-Mahony equation.

You can view this preprint as the “spiritual successor” to my previous work with Patrick Farrell. In Part 1, we showed how one can jointly employ auxiliary variables and finite elements in time to preserve multiple, general conervation laws and dissipation inequalities in our PDE disrcetisations. This was exciting work, as classical approaches for constructing timestepping schemes (such as Runge–Kutta methods and symplectic integrators) typically fail to preserve the behaviour of non-quadratic invariants, and other bespoke structure-preserving integrator were typically limited to a maximum of one preserved quantity of interest.

Now in Part 2, we show just how powerful this idea can be, with two related examples…

Multi-conservative ODEs

Many physical systems have many invariants.

Let me fix ideas with somewhat of a canonical example (one which we consider in the manuscript): the Kepler problem, a simple 2-body gravitional system, e.g. for a planet orbiting a star. Of course energy is conserved; that’s always the case. But there’s also the angular momentum, which encodes the speed of the orbit. And then (less famously) there’s a final conserved invariant of the Runge-Lenz (RL) vector, which encodes the angle of the orbit; conservation of the RL vector is what prevents a planet’s orbit from precessing.

Implicit midpoint would here conserve energy and angular momentum—both are quadratic—both it won’t conserve the non-polynomial RL vector. Naturally then (despite it being commonplace and well loved in the literature) such simulations exhibit some pretty shocking unphysical precession.

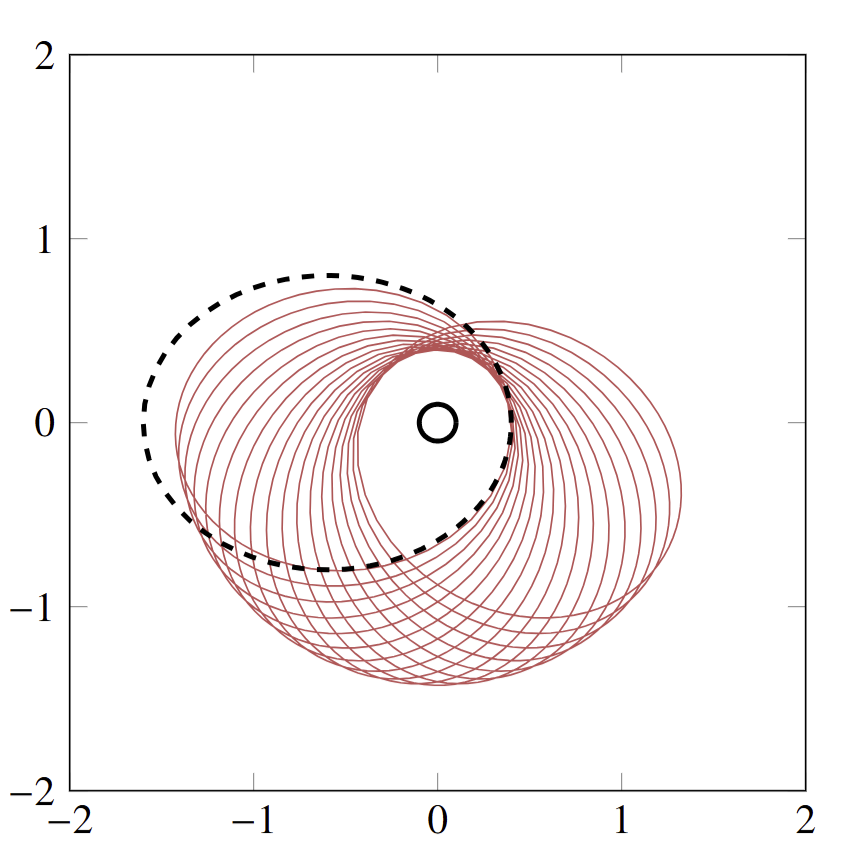
implicit_midpoint

In this manuscript, Patrick Farrell and I employ our auxiliary variable framework to construct an integrator for general ODE systems with multiple invariants that conserves every known invariant.

andrews_farrell

Simulations of the Kepler problem (above) and the Kovalevskaya top show some very substantial improvements in the quality of the numerical solutions.

GENERIC systems

The GENERIC formalism is somewhat of a “grand unified theory” for non-equilibrium thermodynamics. It describes systems that simultaneously exhibit both:

reversible dynamics (like Hamiltonian mechanics) with a conserved energy, and
irreversible dynamics (like friction or heat diffusion) with a generated entropy.

It’s like an extension of Hamiltonian mechanics that doesn’t just incorporate the First Law of Thermodynamics (energy conservation), but the Second Law (entropy generation) too.

FULL DETAILS

The general GENERIC ODE in \(\mathbf{x} : \mathbb{R}_+ \to \mathbb{R}^d\) is \[ \dot{\mathbf{x}} = L(\mathbf{x})\nabla E(\mathbf{x}) + M(\mathbf{x})\nabla S(\mathbf{x}). \] Here, \(E, S : \mathbb{R}^d \to \mathbb{R}\) are the (conserved) energy and (non-decreasing) entropy, and \(L, M : \mathbb{R}^d \to \mathbb{R}^{d\times d}\) are the skew-symmetric (Poisson) matrix and positive semidefinite (friction) matrix. With the following orthogonality conditions, \[ \nabla S(\mathbf{x})^\top L(\mathbf{x}) = 0, \qquad \nabla H(\mathbf{x})^\top M(\mathbf{x}) = 0, \] the conservation of \(E\) and non-dissipation of \(S\) can be identified by testing against \(\nabla E\) and \(\nabla S\) respectively. Extending to PDEs is fiddly (for the introduction of Fréchet derivatives) but similar.

As the name suggests, this is extremely general. Examples of such systems include:

the compressible Navier–Stokes equations;
the Boltzmann equation;
pretty much any irreversible thermodynamic system.

Simulating these accurately is tricky. Despite being a simple modification to a Hamiltonian system, the introduced dissipative component means symplectic integrators can really fail quite badly.

In the manuscript, for example, we consider a simple dissipative thermodynamic engine, that should in theory slow to a halt. Using implicit midpoint (red) however, we find the numerical solution can perform as bad as to accelerate faster and faster and FASTER, until the solver fails (and presumably the engine explodes).

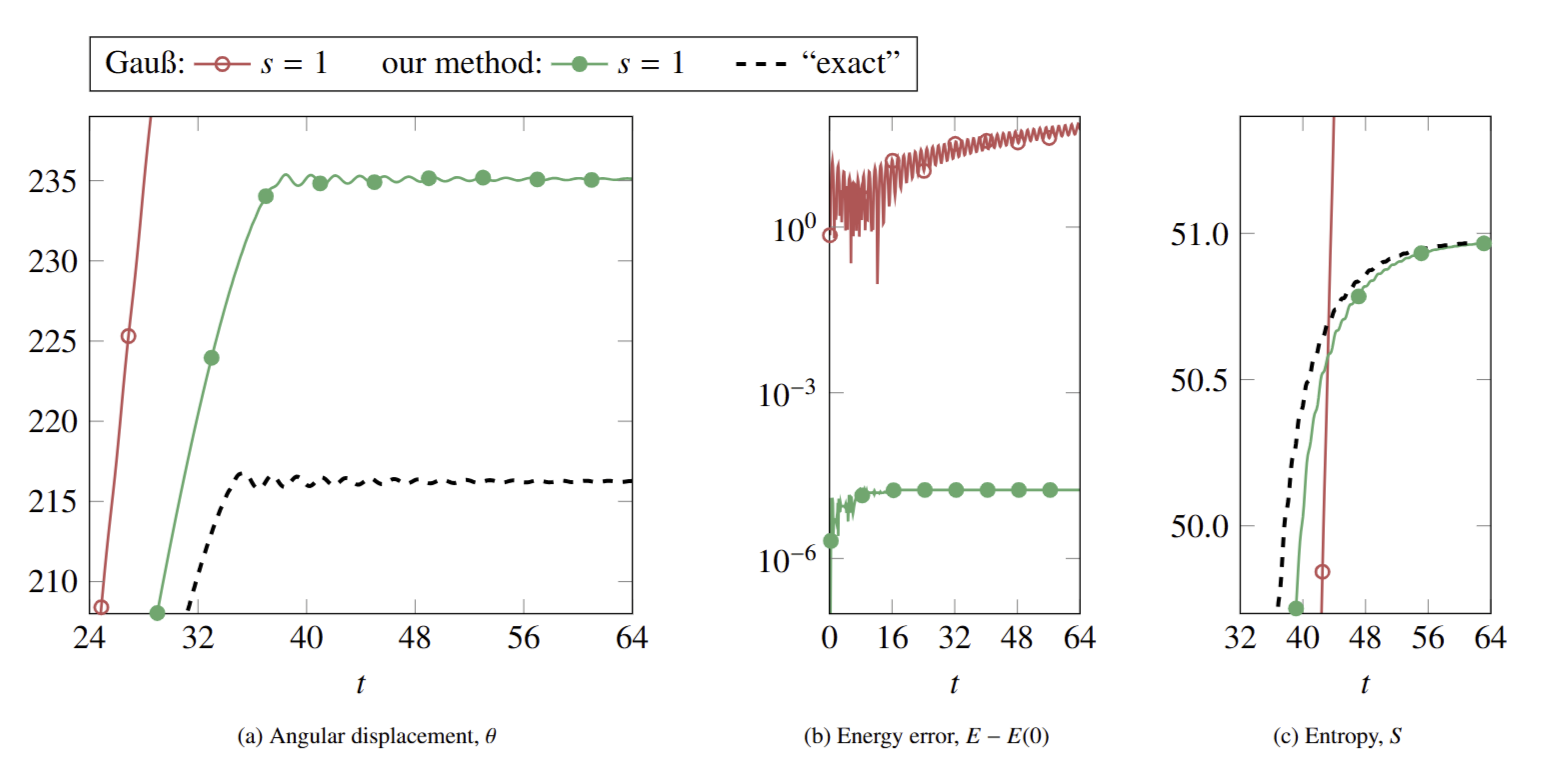
engine

We apply the framework from our previous paper to construct numerical integrators that preserve both the conservative and dissipative structures. As such, we have a general way to construct structure-preserving ODE integrators and finite element methods for any of the above systems. You can see the results with our comparable 1-stage scheme (green) in the figure above; nice and dissipative! For a PDE example, the manuscript presents an integrator for the Boltzmann equation that preserves both the conservation of energy and generation of entropy.

Preserving these properties is crucial for accurately capturing the dynamics of these systems.

CHECK OUT ON ARXIV!

We would both gladly discuss it further!

VIDEOS

Check out Patrick’s Langtangen Seminar (22.APR.2025) at Simula below:

His earlier ACM Colloquium (13.NOV.2024) at the University of Edinburgh and Heriot-Watt University can be found here.

As stated above, the construction of both the schemes in this manuscript employs the framework presented in my earlier work with Patrick Farrell, on conservative and dissipative finite element integrators.

Problem	Reward
Conservative integrators for PDEs with arbitrarily many invariants	★★★★★
Dissipative integrators for ODEs with arbitrarily many dissipated quantities	★★★★★
Application of the auxiliary variable framework to a viscoelastic fluid system	★★☆☆☆
Structure-preserving integrators for compressible MHD	★☆☆☆☆

TALKS

2026

ECCOMAS WCCM, Munich

⬆️ UPCOMING ⬆️

2025

⬇️ PAST ⬇️

Biennial Numerical Analysis Conference, University of Strathclyde
Numerical Mathematics & Scientific Computing Seminar, Rice University
SIAM CSE, Fort Worth, Texas
Scientific Computing Seminar, Brown Unversity

2024

External ("tiny desk") Seminar, Rice University
Computing Division Technical Meeting, UKAEA
Firedrake User Meeting, University of Oxford
PDEsoft, University of Cambridge
Finite Element Fair, University College London (UCL)
Exploiting Algebraic and Geometric Structure in Time-integration Methods workshop, University of Pisa
UKAEA PhD Student Engagement Day, UKAEA
Junior Applied Mathematics Seminar, University of Warwick

2023

ICIAM, Waseda University
Numerical Analysis Group Internal Seminar, University of Oxford
Junior Applied Mathematics Seminar, University of Oxford
Met Office Presentation, University of Oxford